type
Post
status
Published
date
Aug 28, 2022
slug
topology-sort
summary
拓扑排序算法介绍
tags
算法
category
技术分享
icon
password
URL
背景
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
输入:有向无环图G
输出:结点序列;对于所有的边<u,v>∈E(G),结点u排在v前面。
相关应用:程序处理流程的排序,大学课程表学习顺序问题
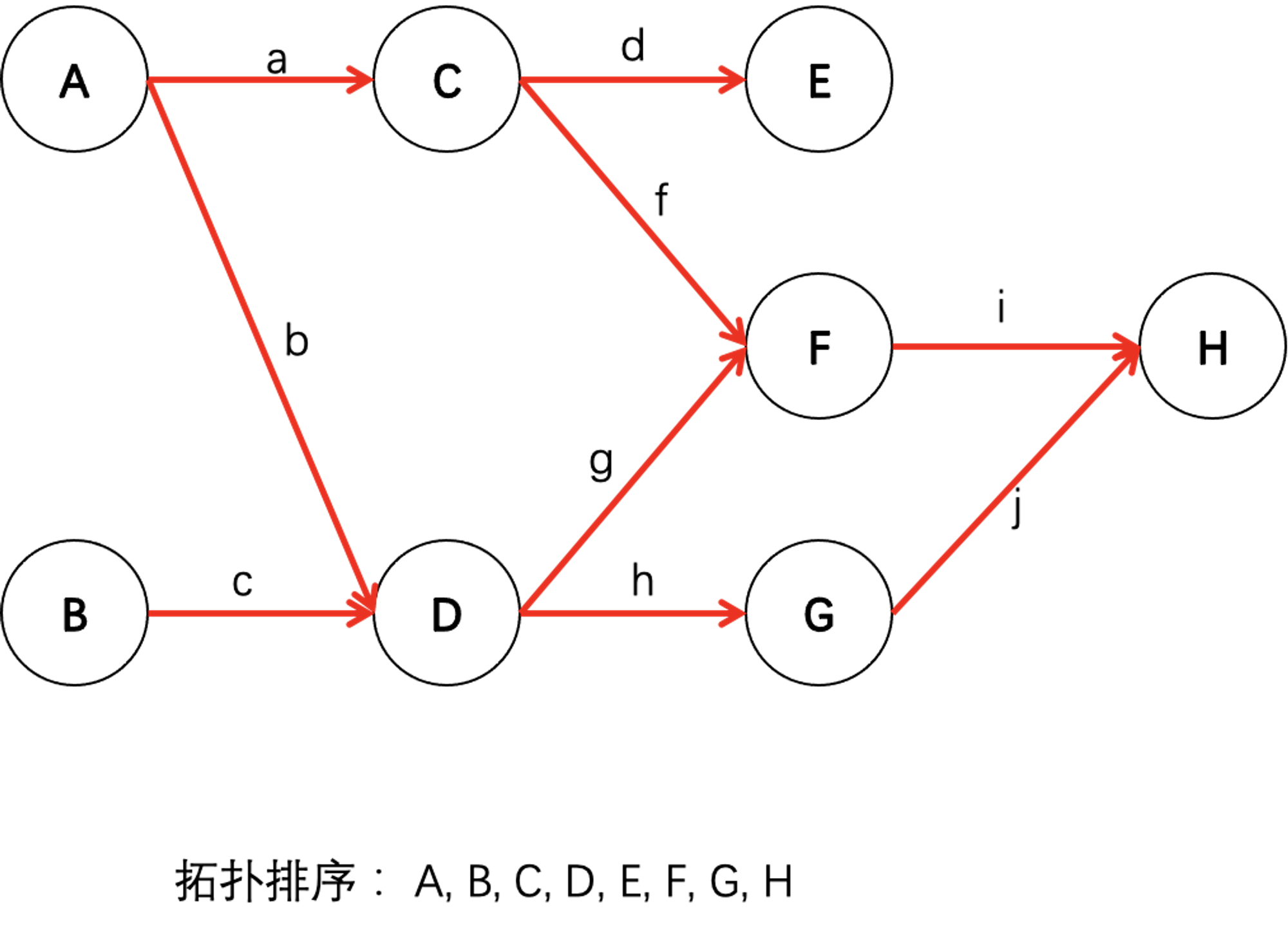
原理
排序原理:只要保证指向该结点的节点都被遍历过,当前节点方可访问。
如何确定结点可以访问呢?最简单的情况是,结点的入度为0,即没有其他结点指向该结点。
可以利用这个特性进行拓扑排序,只需要把访问过的节点和由该节点出发的边删除后,在新的图中入度为0的节点为可访问的结点。
如上图所示,第一步可访问的结点为A和B,因为其入度为0,可以首先访问A和B,之后把结点A、B边a、b删除,得到新的图。
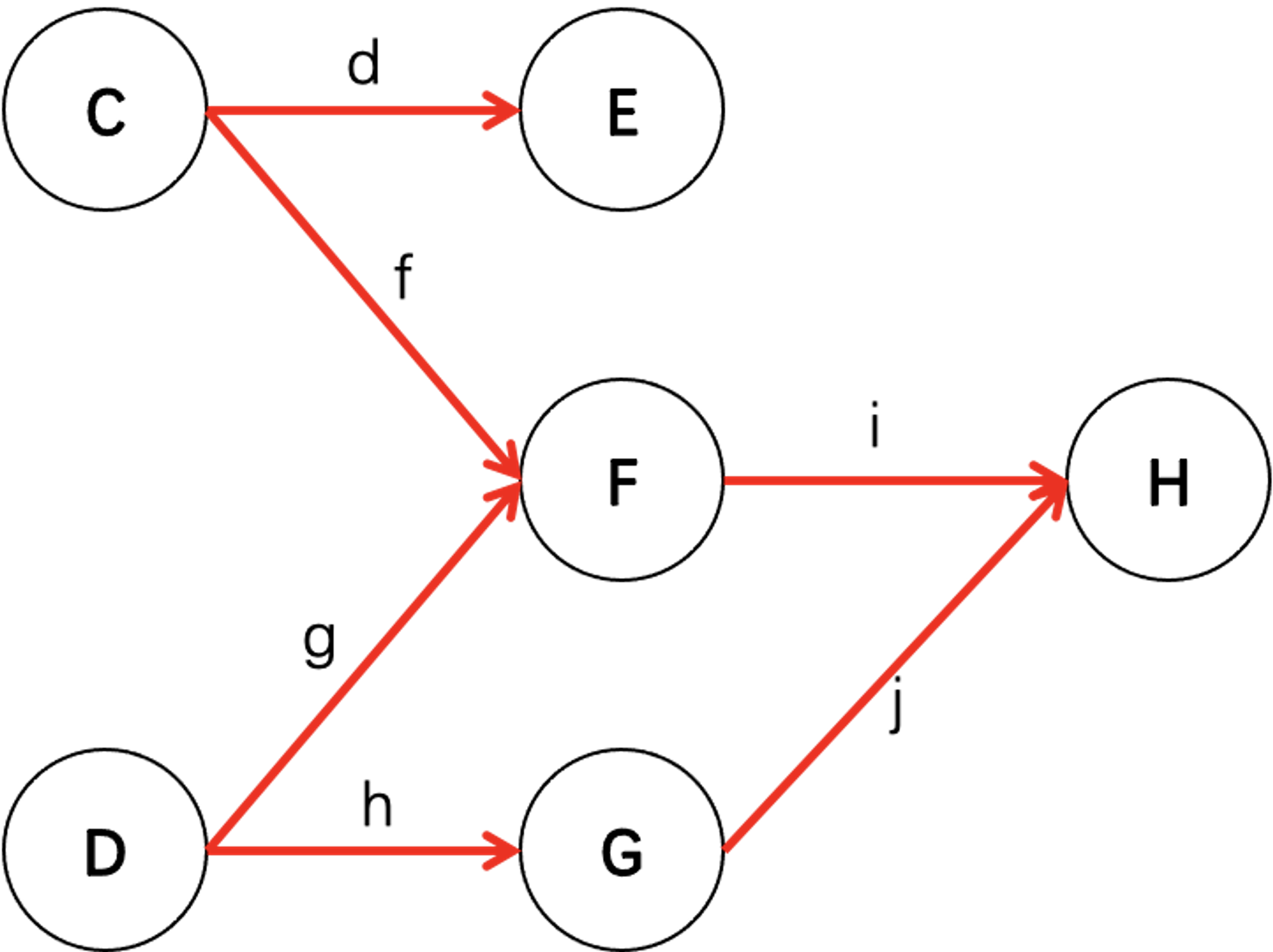
访问C和D,之后把以结点C、D出发的边d、f、g、h删除,得到新的图。
访问E、F和G,之后把以结点E、F和G出发的边i、j删除,得到新的图。
访问H,这时候图已经没有结点了,结束排序。
代码实现
#!/usr/bin/python3 # -*- coding: utf-8 -*- # Created by Ross def get_in_degreee_zero(graph, visited): """ get node where node's in degress equal 0. """ node2in_degree = {node: 0 for node in graph.keys() if node not in visited} for _from, to_nodes in graph.items(): if _from in visited: continue for to_node in to_nodes: node2in_degree[to_node] += 1 return [node for node, in_degress in node2in_degree.items() if in_degress == 0] def topological_sort(graph): """topological sort""" result = [] visited = set() in_degress_zero_nodes = get_in_degreee_zero(graph, visited) while in_degress_zero_nodes: result.extend(in_degress_zero_nodes) visited.update(in_degress_zero_nodes) in_degress_zero_nodes = get_in_degreee_zero(graph, visited) return result if __name__ == '__main__': g = { 'A': ['C', 'D'], 'B': ['D'], 'C': ['E', 'F'], 'D': ['F', 'G'], 'E': [], 'F': ['H'], 'G': ['H'], 'H': [] } res = topological_sort(g) print(res)
- 作者:Ross
- 链接:https://ross.selfcoding.cn/article/topology-sort
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
